前缀和数组
用于求出数组中索引区间元素和
题目
一维数组前缀和
Leetcode303:区域和检索-数组不可变
给定一个整数数组 nums,处理以下类型的多个查询:
- 计算索引
left和right(包含left和right)之间的nums元素的 和 ,其中left <= right
实现 NumArray 类:
NumArray(int[] nums)使用数组nums初始化对象int sumRange(int i, int j)返回数组nums中索引left和right之间的元素的 总和 ,包含left和right两点(也就是nums[left] + nums[left + 1] + ... + nums[right])
示例 1:
1 | 输入: |
提示:
1 <= nums.length <= 104-105 <= nums[i] <= 1050 <= i <= j < nums.length- 最多调用
104次sumRange方法
实现代码
1 | class NumArray { |
解题思路
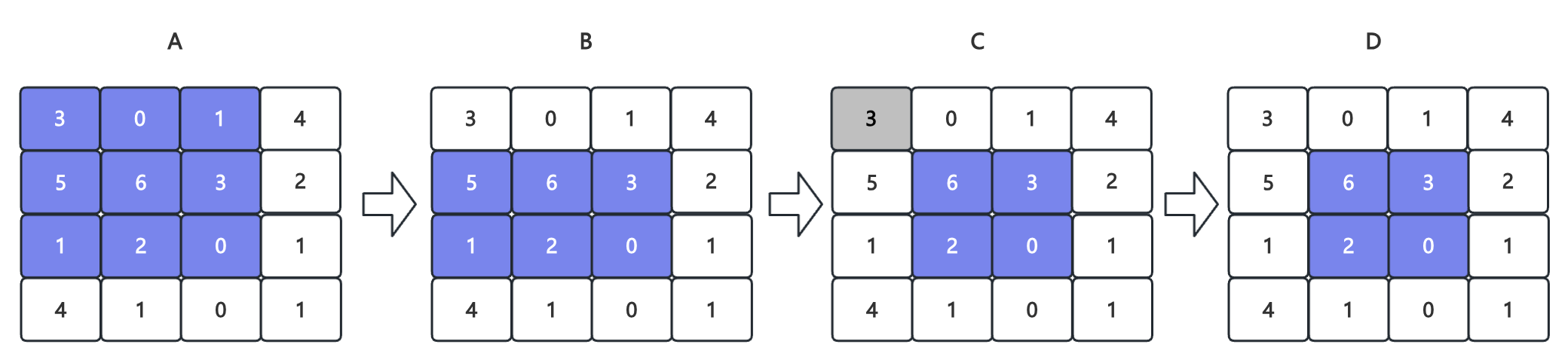
通过构建一个新数组,存储0索引位置到指定索引位置区间元素的和,如:
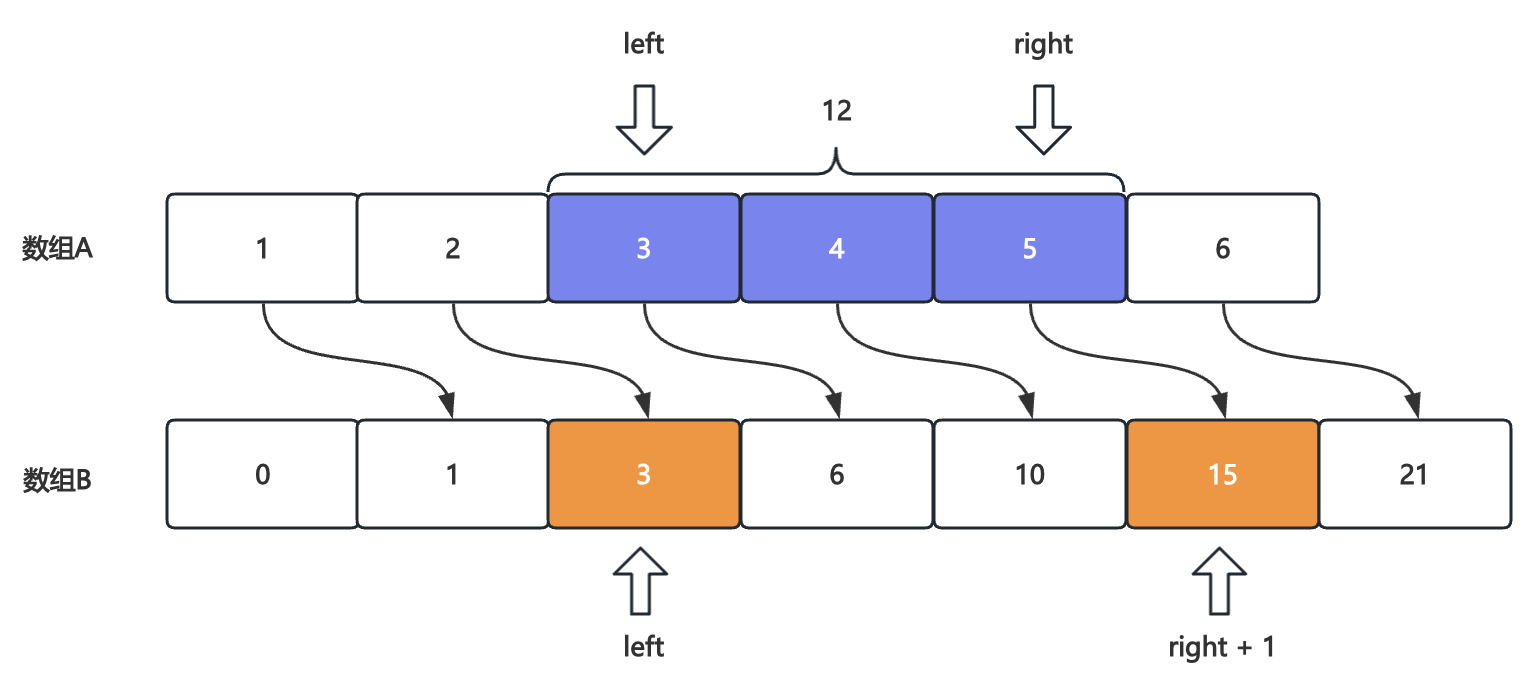
数组B用于存储数组A从索引0到索引n区间的元素和,如数组B索引2 = 数组A索引0 + 数组A索引1,求索引区间元素和则是:
数组A[left -> right] = 数组B[right + 1] - 数组B[left]
注意:构建元素和的数组必须要比原数组大小多1
假设数组A和数组B相同长度,如下:
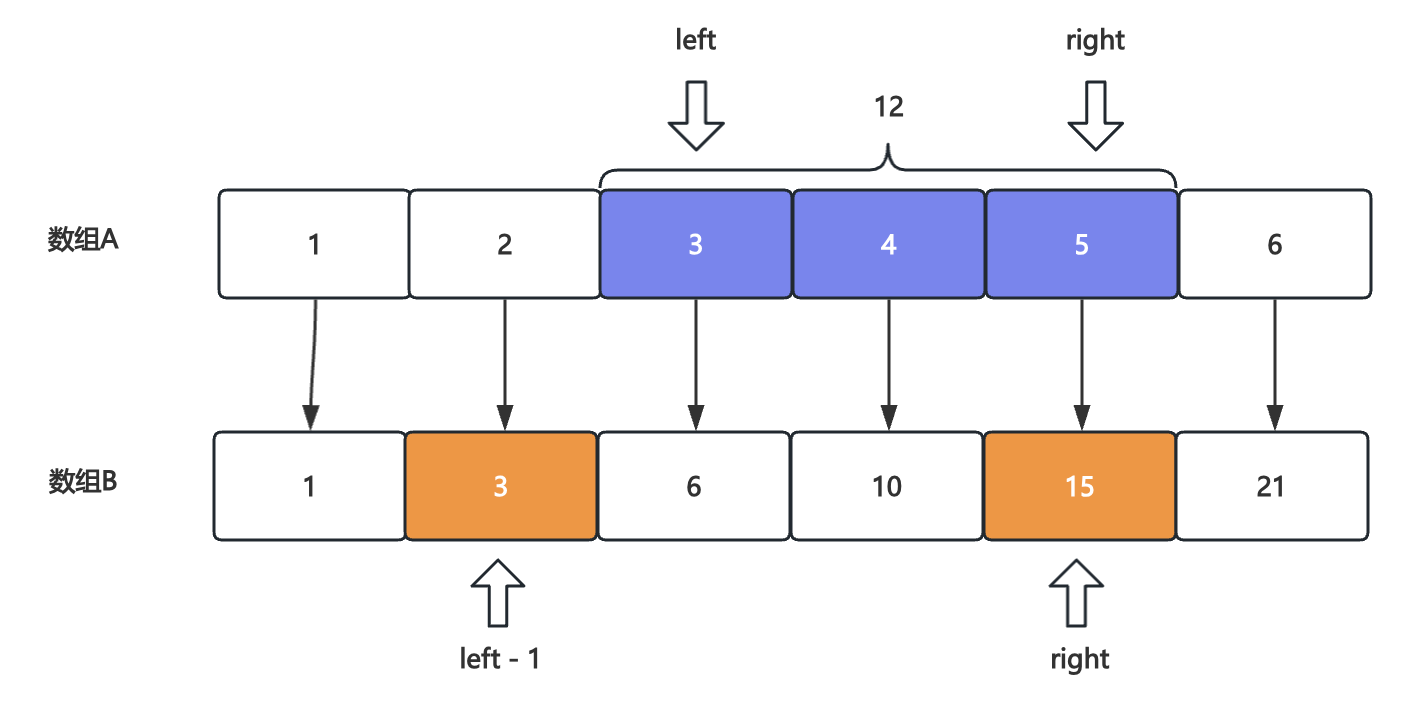
区间范围元素和:
数组A[left -> right] = 数组B[right] - 数组B[left - 1]
那么如果是求数组A索引区间0到开始的元素和,就需要判断边界值
时间复杂度
时间组成:
假设nums长度为n
- 构建前缀和,遍历nums数组:
O(n) - 计算区间和:
O(1)
总的时间:题目的目的是计算索引范围和,所以构造前缀和的时间不算进来,因此时间复杂度为O(1)
空间复杂度
空间组成:
- 存储元素区间和的数组sum:
O(n + 1)
总的空间:O(n)
二维数组前缀和
Leetcode304:二维区域和检索-矩阵不可变
给定一个二维矩阵 matrix,以下类型的多个请求:
- 计算其子矩形范围内元素的总和,该子矩阵的 左上角 为
(row1, col1),右下角 为(row2, col2)。
实现 NumMatrix 类:
NumMatrix(int[][] matrix)给定整数矩阵matrix进行初始化int sumRegion(int row1, int col1, int row2, int col2)返回 左上角(row1, col1)、右下角(row2, col2)所描述的子矩阵的元素 总和 。
示例 1:
1 | 输入: |
提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 200-105 <= matrix[i][j] <= 1050 <= row1 <= row2 < m0 <= col1 <= col2 < n- 最多调用
104次sumRegion方法
实现代码
有两种解法:
- 当做一维数组前缀和处理,遍历每行,进行相加;
- 构建一个二维数组前缀和;
第一种方式的时间复杂度为
O(n),但是第二种为O(1),所以下面使用第二种来讲解;
1 | class NumMatrix { |
解题思路
这种解法用到数学方式,如下:
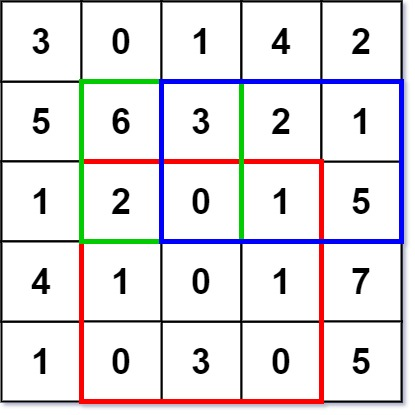
如上图,假设求中间范围[1,1] -> [2,2]的元素和[6,3,2,0],它等于减去上面部分的元素和,再减去左边部分的元素和,再加上左上角部分的元素和,这三部分都是以[0,0]作为起点,假设定义原点[0,0]到任意索引位置的元素和为matrixSum,则会存在以下公式:
matrixSum[i , j] = matrixSum[i-1 , j] + matrixSum[i , j-1] - matrixSum[i-1 , j-1] + matrix[i , j]
matrixSum[i , j] :[0,0] -> [i,j]的全部元素和
matrixSum[i-1 , j] :上边部分的元素和
matrixSum[i , j-1] :左边部分的元素和
matrixSum[i-1 , j-1] :左上角部分的元素和
matrix[i , j]:本身需要求的那块区域元素和
和一维数组一样,为了方便处理边界问题,matrixSum定义也会比matrix大1,所以公式则改为:
matrixSum[i+1 , j+1] = matrixSum[i , j+1] + matrixSum[i+1 , j] - matrixSum[i , j] + matrix[i , j]
那么当我们求任意区域的元素,只要提供区域的左上角索引位置和右下角索引位置,就能通过以下公式算出:
假设左上角索引位置[row1,col1],右下角索引位置[row2,col2]:
matrixSum[row2 + 1][col2 + 1] - matrixSum[row1][col2 + 1] - matrixSum[row2 + 1][col1]
matrixSum[row2 + 1][col2 + 1] :全部元素和
matrixSum[row1][col2 + 1] :上边部分的元素和
matrixSum[row2 :左边部分的元素和
matrixSum[row2 + 1][col1]:左上角部分的元素和
时间复杂度
时间:
- 计算区间和:
O(1)
总的时间:O(1)
空间复杂度
额外空间:
- matrixSum:
O(n+1)
总空间:O(n)