【力扣54】螺旋矩阵

题目

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

示例 1：

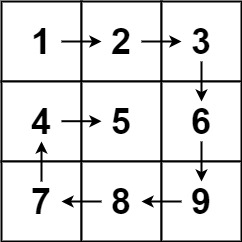
1 2	输入：matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出：[1,2,3,6,9,8,7,4,5]

示例 2：

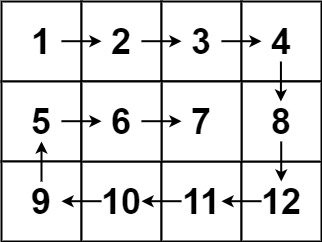
1 2	输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]] 输出：[1,2,3,4,8,12,11,10,9,5,6,7]

提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 10
-100 <= matrix[i][j] <= 100

实现代码

class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        // 思路：定义四个点作为起始遍历条件，慢慢缩圈遍历
        // 行数
        int rowCount = matrix.length;
        // 列数
        int columnCount = matrix[0].length;
        // 上边
        int top = 0;
        // 右边
        int right = 0;
        // 左下
        int left = rowCount - 1;
        // 右下
        int down = columnCount - 1;

        List<Integer> list = new ArrayList<>();
        while (list.size() < (rowCount * columnCount)) {
            // 遍历上边
            for (int i = top; i <= down; i++) {
                list.add(matrix[right][i]);
                if (list.size() == rowCount * columnCount) {
                    return list;
                }
            }
            // 上边往下移
            right += 1;
            // 遍历右边
            for (int i = right; i <= left; i++) {
                list.add(matrix[i][down]);
                if (list.size() == rowCount * columnCount) {
                    return list;
                }
            }
            // 右边往左移
            down -= 1;
            // 遍历下边
            for (int i = down; i >= top; i--) {
                list.add(matrix[left][i]);
                if (list.size() == rowCount * columnCount) {
                    return list;
                }
            }
            // 下边往上移
            left -= 1;
            // 遍历左边
            for (int i = left; i >= right; i--) {
                list.add(matrix[i][top]);
                if (list.size() == rowCount * columnCount) {
                    return list;
                }
            }
            // 左边往右移
            top += 1;
        }
        return list;
    }
}

核心点

遍历线路：左上往右遍历，右上往下遍历，右下往左遍历，左下往上遍历；
当一条边遍历完之后，可以向边的反方向移动一步，两个作用：
1. 向内收缩
2. 避免重复遍历
如下代码
1
2
3
4
5
6
7
8
9
// 遍历上边
for (int i = top; i <= down; i++) {
list.add(matrix[right][i]);
if (list.size() == rowCount * columnCount) {
return list;
}
}
// 上边往下移
right += 1;
当遍历完上边之后，通过right += 1;将上边往下移，向内收缩，同时也将右边的起始遍历点往下推了一格（因为右上那个点已经在遍历上边时被遍历过了）