【力扣47】全排列II

题目

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

示例 1：

输入：nums = [1,1,2]
输出：
[[1,1,2],
 [1,2,1],
 [2,1,1]]

示例 2：

1 2	输入：nums = [1,2,3] 输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

提示：

1 <= nums.length <= 8
-10 <= nums[i] <= 10

实现代码

使用DFS实现回溯算法 + 排序 + 剪枝

class Solution {
    List<List<Integer>> traceList = new LinkedList<>();
    LinkedList<Integer> trace = new LinkedList<>();

    public List<List<Integer>> permuteUnique(int[] nums) {

        // 记录当前走的路径
        boolean[] used = new boolean[nums.length];
        // 排序
        Arrays.sort(nums);
        backtrack(nums, used);
        return traceList;
    }

    private void backtrack(int[] nums, boolean[] used) {

        if (trace.size() == nums.length) {
            traceList.add(new LinkedList<>(trace));
            return;
        }
        for (int i = 0; i < nums.length; i++) {
            // 解决相同元素问题
            if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {
                continue;
            }
            if (used[i]) {
                continue;
            }
            used[i] = true;
            trace.addLast(nums[i]);
            backtrack(nums, used);
            trace.removeLast();
            used[i] = false;
        }
    }
}

核心思路

这道题的关键在于去重，因为数组中可能包含重复元素，但最终结果不能有重复的组合。

解决方案：

排序：将相同的元素聚集在一起，便于去重处理
去重逻辑/剪枝优化：if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) continue;
- 在同一层递归中，跳过重复的元素
- 但在不同层递归中，允许使用重复元素

这里有个很重要的点：为什么要判断!used[i - 1]？

之前做子集相关题的时候（见：力扣90），如果元素存在重复，并且要求结果不能包含重复的子集，只需判断i > n && nums[i] == nums[i - 1] 即可，但是为什么在排列问题中判断重复为什么还要加 !used[i - 1]？

先看图（部分节点已省略，为了更好的讲解，只画了1a那一小部分）：

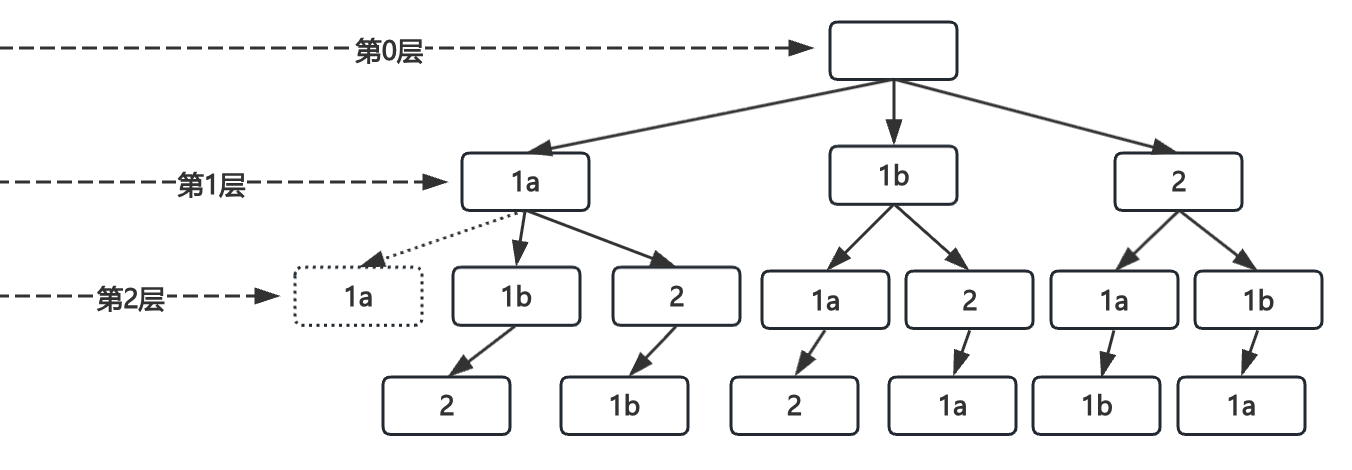
上图是数组构建排序状态的树结构，假设存在数组nums = [1, 1, 2]，其中第一个1和第二个1分别记为1a和1b，元素存在重复，并且结果不包含重复子集，只需要将元素排序后相邻的相同元素只处理一个即可，也就是通过i > 0 && nums[i] == nums[i - 1] 代码剪枝优化进行去重，但是，如果仅仅是这样，会存在一个问题：

先贴下代码：

for (int i = 0; i < nums.length; i++) {
    // 解决相同元素问题
    if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {
        continue;
    }
    if (used[i]) {
        continue;
    }
    used[i] = true;
    trace.addLast(nums[i]);
    backtrack(nums, used);
    trace.removeLast();
    used[i] = false;
}

比如：

当前处于第1层

开始处理子节点1a，状态如下：

i = 0
nums[0] = 1a
used[0] = false

开始执行代码：

不符合i > 0 && nums[i] == nums[i - 1]条件，跳过往下执行；
不符合if (used[i])条件，跳过往下执行；
直到执行backtrack(nums, used);，进入在一层；

进入第二层

同样开始处理子节点1a，状态如下：

i = 0
nums[0] = 1a
used[0] = true

开始执行代码：

不符合i > 0 && nums[i] == nums[i - 1]条件，跳过往下执行；
符合if (used[i])条件，直接continue；

开始处理子节点1b，当前状态如下：

i = 1
nums[1] = 1b
used[1] = false

开始执行代码：

因为num[1] == num[0]，符合i > 0 && nums[i] == nums[i - 1]条件，直接continue；

问题就在这出现了，正常是不应跳过1b的，那么为什么会这样呢？

问题点在于做i > 0 && nums[i] == nums[i - 1]判断的时候，把已经使用的1a也考虑进去了，1a已经在上层用过了，对应的used[0] = true，所以需要再加一个条件!used[i - 1]，也就是在处理1b的时候，进行i > 0 && nums[i] == nums[i - 1]校验时需要考虑左边这个是不是父节点值，如果是就不能跳过；

时间复杂度

在最坏情况下，需要遍历所有可能的排列。对于长度为n的数组，如果不考虑重复元素，全排列的数量为n!。由于数组中可能包含重复元素，实际的不重复排列数量会少于或等于n!。

状态空间：不重复的排列数量，记为P（P ≤ n!）
实际剪枝效果：
- 排序后的去重剪枝：当if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1])时直接continue，避免重复状态的尝试，大大减少了搜索空间；
每个有效状态的处理时间：复制当前路径到结果集，时间复杂度为O(n)，