题目

给你一个整数数组 nums ，其中可能包含重复元素，请你返回该数组所有可能的 子集（幂集）。

解集 不能 包含重复的子集。返回的解集中，子集可以按 任意顺序 排列。

示例 1：

1
2
输入：nums = [1,2,2]
输出：[[],[1],[1,2],[1,2,2],[2],[2,2]]

示例 2：

1
2
输入：nums = [0]
输出：[[],[0]]

提示：

  • 1 <= nums.length <= 10
  • -10 <= nums[i] <= 10

实现代码

使用DFS实现回溯算法，因为元素会重复，所以需要判断每个节点下的子节点必须只能处理一个

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
    List<List<Integer>> traceList = new LinkedList<>();

    LinkedList<Integer> trace = new LinkedList<>();

    public List<List<Integer>> subsetsWithDup(int[] nums) {

        Arrays.sort(nums);
        backtrack(nums, 0);
        return traceList;
    }

    private void backtrack(int[] nums, int n) {

        traceList.add(new LinkedList<>(trace));
        for (int i = n; i < nums.length; i++) {
            // 同一个节点下子节点相同值只能处理一个
            if (i > n && nums[i] == nums[i - 1]) {
                continue;
            }
            trace.addLast(nums[i]);

            backtrack(nums, i + 1);
            trace.removeLast();
        }
    }
}

假设nums = [1, 2, 3, 2]，那么构建的树如下：

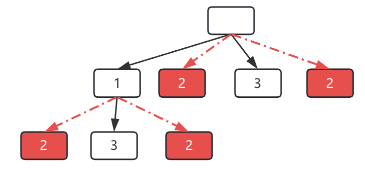
image-20250926230955475

很显然，相同的元素存在同一层就会导致子集重复

时间复杂度

假设数组元素数量为n，那么子集的数量就为2^n，再看每个节点的处理情况，tranceList.add(new LinkedList<>(trance));，每次都需要将trance所有的元素复制给一个新链表集合，时间复杂度为n，所以总时间复杂度为O(n*2^n)；

空间复杂度

主要的额外空间消耗来自：

  1. traceList：存储所有子集，共有2^n个子集，每个子集平均长度为n/2，所以空间复杂度为O(n*2^n)
  2. trace：递归过程中存储当前路径，最大深度为n，空间复杂度为O(n)
  3. 递归调用栈：最大深度为n，空间复杂度为O(n)

因此总的空间复杂度为O(n*2^n)，如果不计算返回空间的话就是O(n)