【力扣773】滑动谜题

题目

在一个 2 x 3 的板上（board）有 5 块砖瓦，用数字 1~5 来表示, 以及一块空缺用 0 来表示。一次移动定义为选择 0 与一个相邻的数字（上下左右）进行交换.

最终当板 board 的结果是 [[1,2,3],[4,5,0]] 谜板被解开。

给出一个谜板的初始状态 board ，返回最少可以通过多少次移动解开谜板，如果不能解开谜板，则返回 -1 。

示例 1：

1
2
3

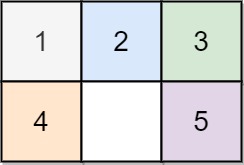
输入：board = [[1,2,3],[4,0,5]]
输出：1
解释：交换 0 和 5 ，1 步完成

示例 2:

1
2
3

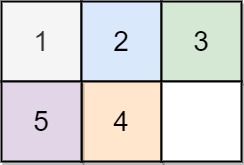
输入：board = [[1,2,3],[5,4,0]]
输出：-1
解释：没有办法完成谜板

示例 3:

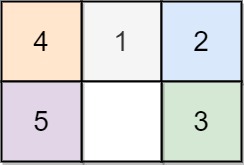
输入：board = [[4,1,2],[5,0,3]]
输出：5
解释：
最少完成谜板的最少移动次数是 5 ，
一种移动路径:
尚未移动: [[4,1,2],[5,0,3]]
移动 1 次: [[4,1,2],[0,5,3]]
移动 2 次: [[0,1,2],[4,5,3]]
移动 3 次: [[1,0,2],[4,5,3]]
移动 4 次: [[1,2,0],[4,5,3]]
移动 5 次: [[1,2,3],[4,5,0]]

提示：

board.length == 2
board[i].length == 3
0 <= board[i][j] <= 5
board[i][j] 中每个值都不同

实现代码

广度优先算法（BFS），0在不同位置所相邻的数字块为树的分支，因为是求最值，所以使用BFS算法

public int slidingPuzzle(int[][] board) {

    // 预定义每个位置的相邻位置索引（2x3网格按行展开为一维数组）
    int[][] adjoinIndexArray = new int[][]{
        {1,3},      // 位置0的相邻位置：右(1)、下(3)
        {0,2,4},    // 位置1的相邻位置：左(0)、右(2)、下(4)
        {1,5},      // 位置2的相邻位置：左(1)、下(5)
        {0,4},      // 位置3的相邻位置：上(0)、右(4)
        {1,3,5},    // 位置4的相邻位置：上(1)、左(3)、右(5)
        {2,4}};     // 位置5的相邻位置：上(2)、左(4)
    
    // 记录已访问的状态，避免重复搜索
    Set<String> visited = new HashSet<>();
    // 将初始状态转换为字符串形式
    String initialState = array2Str(board);
    visited.add(initialState);
    
    // BFS队列，存储待处理的状态
    Queue<String> queue = new LinkedList<>();
    queue.offer(initialState);
    
    int steps = 0; // 记录步数
    while (!queue.isEmpty()) {
        int levelSize = queue.size();
        // 处理当前层的所有状态
        for (int i = 0; i < levelSize; i++) {
            String currentState = queue.poll();
            // 检查是否达到目标状态
            if ("123450".equals(currentState)) {
                return steps;
            }
            
            // 找到空格(0)的位置
            int zeroIndex = zeroIndex(currentState);
            // 获取空格可以移动到的相邻位置
            int[] adjoinIndex = adjoinIndexArray[zeroIndex];
            
            // 尝试将空格与每个相邻数字交换
            for (int index : adjoinIndex) {
                String newState = swap(currentState, zeroIndex, index);
                // 如果是新状态，加入队列继续搜索
                if (!visited.contains(newState)) {
                    queue.offer(newState);
                    visited.add(newState);
                }
            }
        }
        steps++; // 完成一层搜索，步数加1
    }
    return -1;
}

/**
     * 数组转字符串
     *
     * @param array
     * @return
     */
private String array2Str(int[][] array) {

    StringBuilder sb = new StringBuilder();
    for (int[] ints : array) {
        for (int anInt : ints) {
            sb.append(anInt);
        }
    }
    return sb.toString();
}

/**
     * 零角标位置
     *
     * @param str
     * @return
     */
private int zeroIndex(String str) {

    char[] charArray = str.toCharArray();
    for (int i = 0; i < charArray.length; i++) {
        char c = charArray[i];
        if (c == '0') {
            return i;
        }
    }
    return -1;
}

/**
     * 位置交换
     *
     * @param str
     * @param zeroIndex
     * @param adjoinIndex
     * @return
     */
private String swap(String str, int zeroIndex, int adjoinIndex) {

    char[] charArray = str.toCharArray();
    char tmp = charArray[zeroIndex];
    charArray[zeroIndex] = charArray[adjoinIndex];
    charArray[adjoinIndex] = tmp;
    return new String(charArray);
}

代码讲解

// 因为题目固定是6个数字块，所以0在不同位置的相邻块的索引直接枚举
int[][] adjoinIndexArray = new int[][]{
    {1,3},
    {0,2,4},
    {1,5},
    {0,4},
    {1,3,5},
    {2,4}};

当0在索引0位置，则相邻块为索引1、3位置；
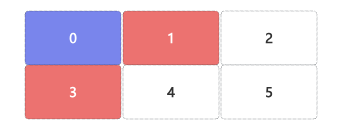
当0在索引1位置，则相邻块为索引0、4、2位置；
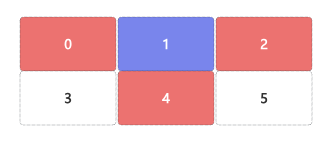
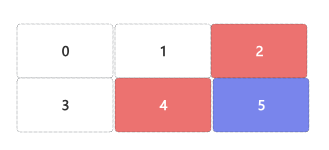
当0在索引2位置，则相邻块为索引1、5位置；
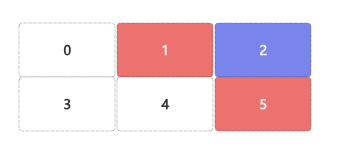
当0在索引3位置，则相邻块为索引0、4位置；
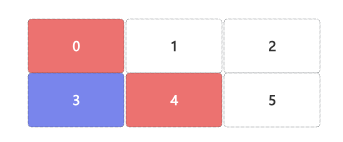
当0在索引4位置，则相邻块为索引3、1、5位置；
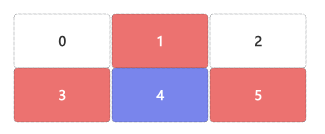
当0在索引5位置，则相邻块为索引2、4位置；

时间复杂度

对于2×3的滑动谜题，总共有6!种可能的状态（因为有6个位置，每个数字0-5都有固定位置）。在最坏情况下，BFS需要遍历所有可能的状态。每个状态需要检查相邻位置（最多4个），每次状态转换的时间复杂度为O(1)（6个）。因此总的时间复杂度为O(6!) = O(720)。虽然在数学上这是一个常数，但对于一般的m×n滑动谜题，时间复杂度应该是O((m×n)!)。