回溯算法
回溯算法模板伪代码
回溯算法本质上还是
DFS算法
1 | LinkedList<Integer> trace = new LinkedList<>(); |
回溯算法解决的问题
回溯算法主要用于解决子集、组合和排列问题,通过对所经过的节点路径进行追踪
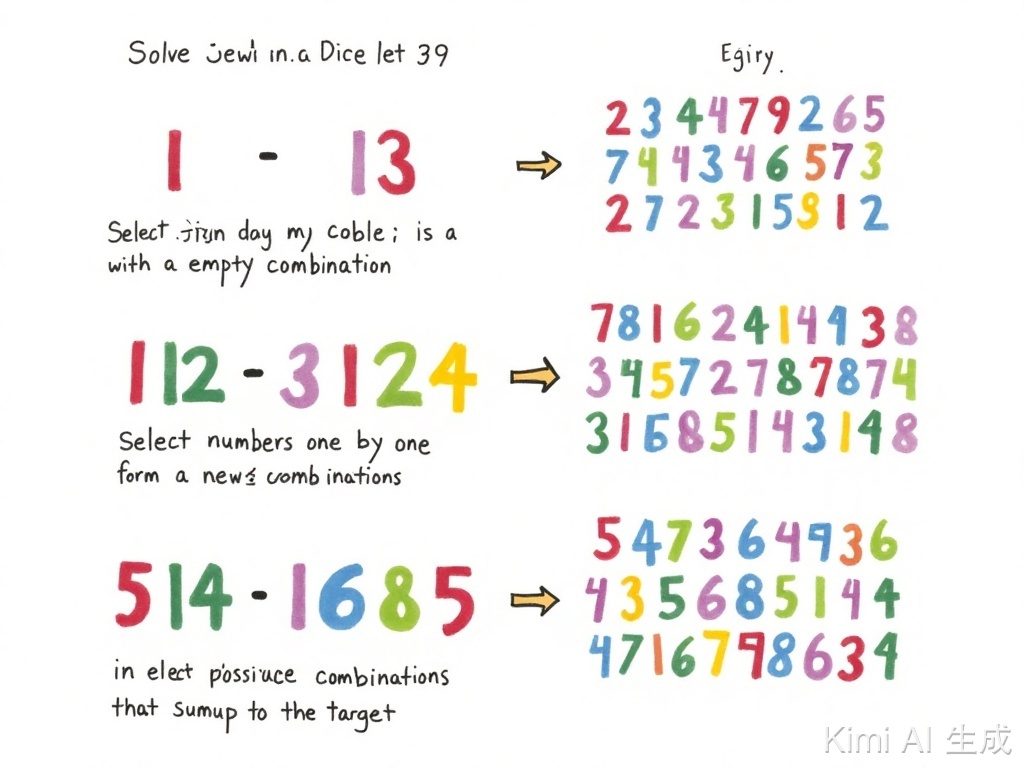
子集问题
子集问题只能
不可重复使用
元素不重复
假设存在数组candidates = [2, 6 ,7],对应子集如下:
[[], [2], [6], [7], [2,6], [2,7], [6,7], [2,6,7]]
通过树构建如下:
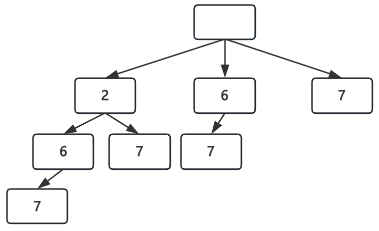
每个子树中,根节点的子节点都是数组当前元素后面的元素,比如节点2,子节点就是[6, 7],节点6,子节点就是[7],也就是说每次遍历子节点都是从数组中当前节点位置的后一个索引位置开始,伪代码如下:
1 | LinkedList<Integer> trace = new LinkedList<>(); |
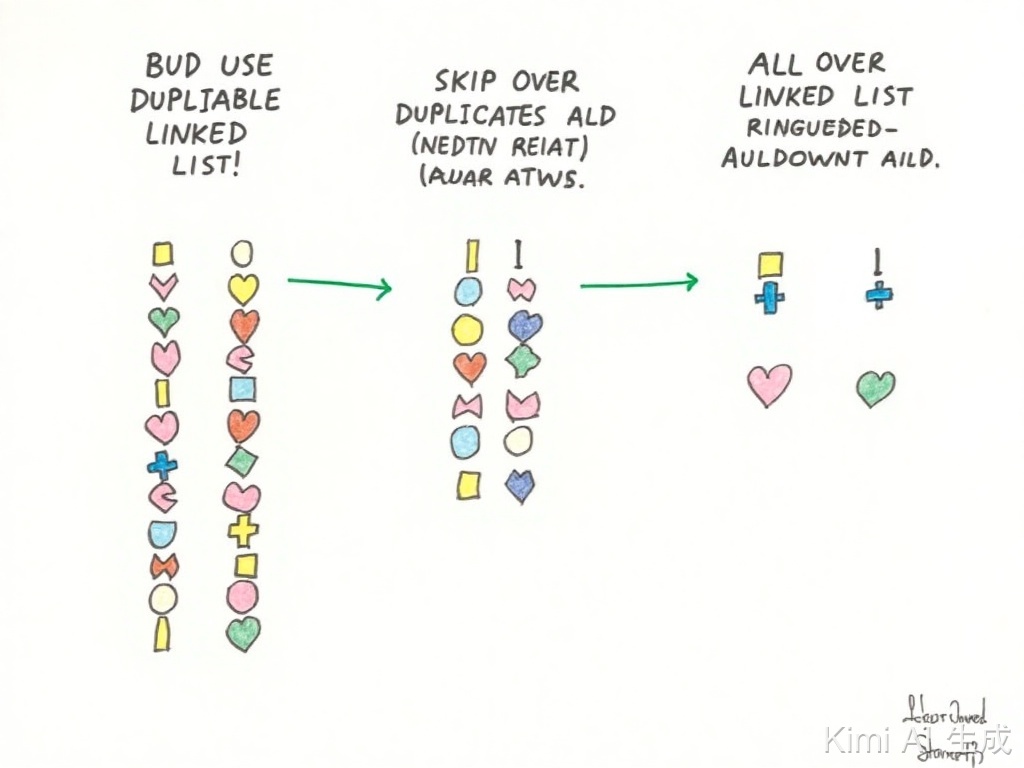
元素重复
如果元素可重复选,那么子集又是怎样的呢?
假设存在数组candidates = [2, 2 ,6],其中元素2存在相同,对应子集如下:
[[], [2], [6], [2,2], [2,6], [2,2,6]]
通过树构建如下:
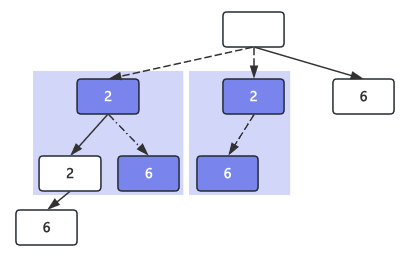
其中子集[2]与[2]重复,[2,6]与[2,6]重复
现在问题是:如何才能去除重复子集呢?
其实看图你会发现,以每个节点作为整个树的子树的根节点,相同元素节点一定是左边子树的子集包含右边同元素节点的子集;
比如左边子树2与右边子树2是相同的元素,其左边子树的子集[[2], [2,2], [2,6]]包含了右边子树所有的子集[[2],[2,6];
既然知道了规律,那么怎么去除呢?
解决方法:只要在处理重复节点的时候直接跳过即可
基于上面的伪代码进行改造,如下:
1 | LinkedList<Integer> trace = new LinkedList<>(); |
组合问题
没有
元素重复,可重复使用的情况,既然元素已经重复了,就不需要再重复选了
元素不重复,不可重复使用
假设存在数组candidates = [2, 6, 8],求元素组合中和等于8的组合集;
树结构如下:
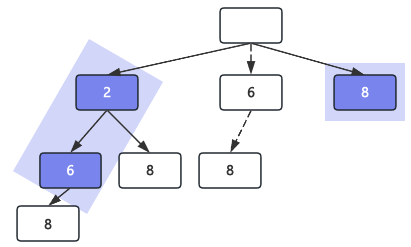
元素不重复,可重复使用
元素重复,不可重复使用
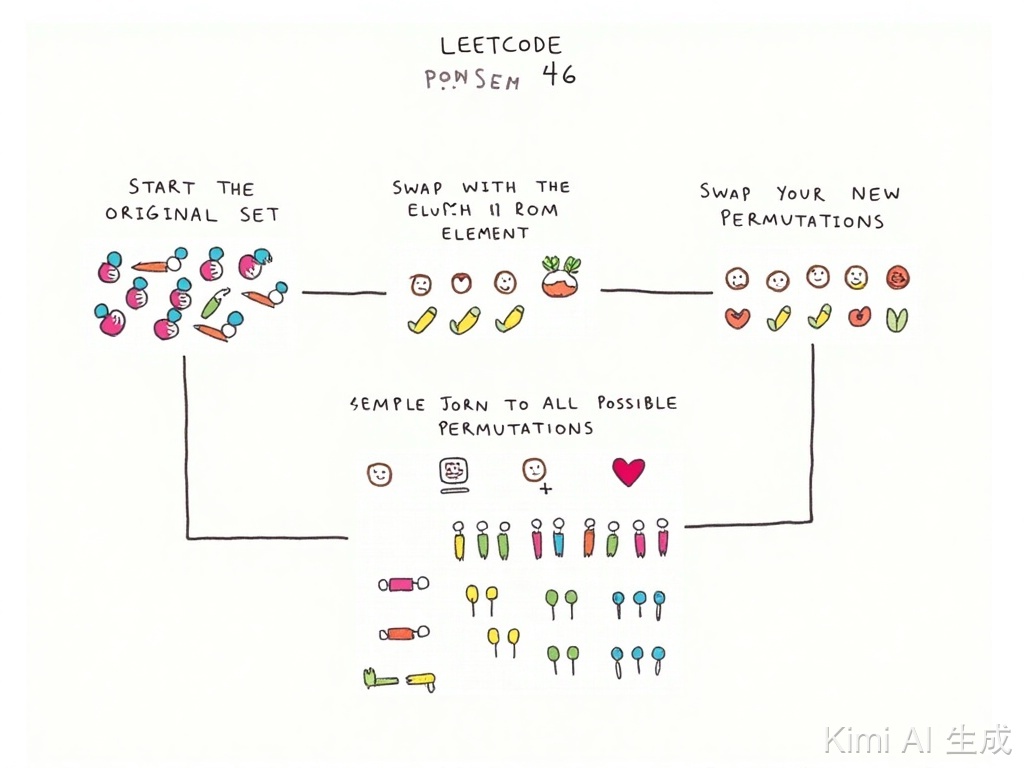
排列问题
排列问题元素
不可重复使用
元素重复
元素不重复
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来源 青柠!
评论