题目

零钱兑换：

给定金额amount和硬币面额值coins[]，求组成金额amount所用的最少硬币数量；

条件

  • 每种面额硬币值的数量不限；

思路

首先确定好状态、选择和状态转换方程式

1、判断是否动态规划问题

  • 最优子结构

    全局最优解包含子问题最优解

    比如：求组成金额100所用的最少硬币数？

    主问题：

    ​ 组成金额100所用的最少硬币数；

    子问题：

    ​ 组成金额99所用的最少硬币数

    ​ 组成金额98所用的最少硬币数

    ​ ……

    主问题最优解答案是最少硬币数，子问题最优解答案也是最少硬币数，求主问题的答案可通过子问题答案进行推导得出

    存在最优子结构的问题不一定是动态规划问题，但动态规划问题一定存在最优子结构；

  • 存在重叠子问题

    同一个子问题被多次计算

    比如在计算金额100的时候，需要计算金额99、98，但是计算金额99的时候也需要计算金额98，计算金额98子问题被多次计算；

2、定义状态

明确动态规划状态函数dp

关键在于定义dp函数表示什么：

dp(i) = 组成金额i所需的最少硬币数

3、推导状态转移方程

根据状态函数的定义dp推导出：

dp(i) = min(dp(i), dp(i-coin) + 1)

代码

实现代码如下：

暴力搜索

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29


public int coinChange(int[] coins, int amount) {

    return recursion(coins, amount);
}

private int recursion(int[] coins, int amount) {

    // 终止条件
    if (amount == 0) {
        return 0;
    }
    if (amount < 0) {
        return -1;
    }
    // 因为要求最少数量，所以这里定义一个最大值
    int minCount = Integer.MAX_VALUE;
    // 遍历每种硬币面额值
    for (int coin : coins) {
        int sub = recursion(coins, amount - coin);
        if(sub == -1){
            continue;
        }
        // 又因为求最少值，所以需要对比不同面额下的最值
        minCount = Math.min(minCount, sub + 1);
    }
    return minCount == Integer.MAX_VALUE ? -1 : minCount;
}

重叠子

存在的问题：

假设amount = 11，coins = [1,3,5,7]，如下图

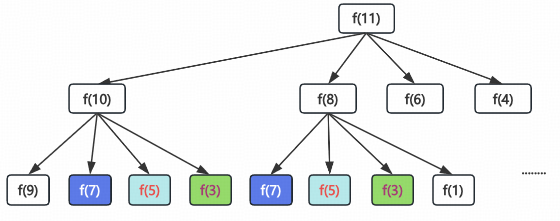
image-20250922084043927

通过树结构进行构建会发现，其中很多都是有重复计算，比如f(7)、f(5)、f(3)……

该问题为重叠子

时间复杂度

假设amount为a，coins为S，那么其时间复杂度为：

S^0+S^1+S^2+S^3+……= O(S^a)

空间复杂度

空间复杂度取决于树的深度，假设每次都是一个硬币，那么空间复杂度就是O(n)

记忆化搜索

因为暴力搜索方式存在重叠子问题，整体性能很差，可以通过将f(amount)进行缓存的方式消除重叠子进行优化，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
int[] dbTable;

public int coinChange(int[] coins, int amount) {

    // 因为金额的取值范围是[0……amount]，所以+1
    dbTable = new int[amount+1];
    // 初始化值
    Arrays.fill(dbTable, -1);
    return recursion(coins, amount);
}

private int recursion(int[] coins, int amount) {

    // 终止条件
    if (amount == 0) {
        return 0;
    }
    if (amount < 0) {
        return -1;
    }
    // 判断缓存
    if(dbTable[amount] != -1){
        return dbTable[amount];
    }
    // 用于比较，目的是获取当前路径在不同硬币面额值的最小值
    int minCount = Integer.MAX_VALUE;
    // 遍历每种硬币面额值
    for (int coin : coins) {
        // 状态转移公式： f(amount) = f(amount - denomination) + 1
        int sub = recursion(coins, amount - coin);
        if (sub == -1) {
            continue;
        }
        // 求最少值，所以需要对比不同面额下的最值
        minCount = Math.min(minCount, sub + 1);
    }
    minCount = minCount == Integer.MAX_VALUE ? -1 : minCount;
    dbTable[amount] = minCount;
    return minCount;
}

时间复杂度

经过加缓存优化之后，由原来的O(S^a) 降到O(S*a)

假设每次都是一元硬币，所以recursion方法需要执行S次，加上每次都需要执行遍历每种面额值，所以就是S*a

空间复杂度

O(N)

动态规划

上面求解问题是通过自顶向下思路来考虑子问题的，也就是：

  • 想要知道最少需要多少硬币数凑成amount金额，需要知道最少多少硬币数凑成amount - 1;

  • 想要知道最少需要多少硬币数凑成amount - 1金额，需要知道最少多少硬币数凑成amount - 2;

  • 想要知道最少需要多少硬币数凑成amount - 2金额，需要知道最少多少硬币数凑成amount - 3;

    以此类推……直到amount = 0，然后进行回朔得出amount对应所需最少的硬币数；

而如果采用动态规划自底向上的思路，则是：

  • 凑成amount = 0的金额，最少需要0个硬币数；

  • 凑成amount = 1的金额，最少需要1个硬币数；

  • 凑成amount = 2的金额，最少需要dp(2)个硬币数；

    以此类推……直到算出amount金额需要的硬币数；

使用动态规划的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
private int coinChange(int[] coins, int amount) {

    if (amount == 0) {
        return 0;
    }
    int[] dpTable = new int[amount + 1];
    // 因为要进行比较，所以不能为-1，又因为dpTable[amount - coin] + 1，
    // 为了防止值溢出，也不能设置为Integer.MAX_VALUE；
    // 设置为amount + 1是因为硬币数不可能大于amount
    Arrays.fill(dpTable, amount + 1);
    // 基值
    dpTable[0] = 0;
    for (int i = 0; i < amount; i++) {
        // 遍历每种硬币面额值
        for (int coin : coins) {
            // 状态转移公式： f(amount) = f(amount - denomination) + 1
            if (i - coin < 0) {
                continue;
            }
            dpTable[i] = Math.min(dpTable[i], dpTable[i - coin] + 1);
        }
    }
    return dpTable[amount] == amount + 1 ? -1 : dpTable[amount];
}

自顶向下与自底向上的区别

自顶向上

缺点：

  • 可能会内存溢出（递归，栈内存溢出）

自底向上

缺点：

  • 当子问题稀疏时，会导致很多无用计算；

比如amount = 11，coins = [3,7,100]，则：

1
2
3
4
5
6
7
8
9
10
11
12
dp[0]  =  [0]
dp[1]  =  []	无用计算
dp[2]  =  []	无用计算
dp[3]  =  [3]
dp[4]  =  []	无用计算
dp[5]  =  []	无用计算
dp[6]  =  [3,3]
dp[7]  =  [7]
dp[8]  =  []	无用计算
dp[9]  =  [3,3,3]
dp[10] =  [3,7]
dp[11] =  []	无用计算

一共需要计算12个子问题，其中有效计算只有5个，

而如果是自顶向上呢?

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
dp[11]
	dp[11 - 3] = 8
	dp[11 - 7] = 4
	dp[11 - 100] = -1(被过滤)
dp[8]
	dp[8-3] = 5
	dp[8-7] = 1
	dp[8-100] = -1(被过滤)
dp[5]
	dp[5-3] = 2
	dp[5-7] = -1(被过滤)
	dp[5-100] = -1(被过滤)
dp[4]
	dp[4-3] = 1
	dp[4-7] = -1(被过滤)
	dp[4-100] = -1(被过滤)
dp[2](被过滤)
dp[1](被过滤)

可知一共会计算dp[11]、dp[8]、dp[5]、dp[4]这四个状态;

很明显，当子问题密集时，使用自底向上效果更好