题目

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1：

img

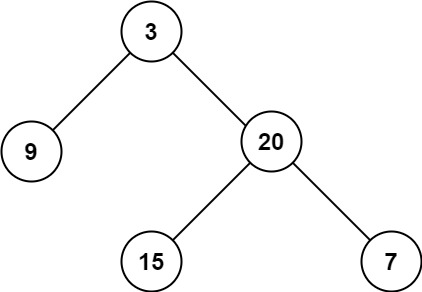
1
2
输入：root = [3,9,20,null,null,15,7]
输出：3

示例 2：

1
2
输入：root = [1,null,2]
输出：2

提示：

  • 树中节点的数量在 [0, 104] 区间内。
  • -100 <= Node.val <= 100

实现代码

通过二叉树的递归遍历（DFS）实现

方式一

前序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {


  int max = 0, n = 0;

  public int maxDepth(TreeNode root) {

    if (root == null) {
      return max;
    }
    traverse(root);
    return max;
  }

  public void traverse(TreeNode root) {

    if (root == null) {
      return;
    }
    // 前往下一个节点之前深度加一
    n++;
    // 计算最大深度
    max = Math.max(max, n);
    maxDepth(root.left);
    maxDepth(root.right);
    // 退出之前减一
    n--;
  }
}

方式二

后序遍历

1
2
3
4
5
6
7
8
9
10
public int maxDepth(TreeNode root) {

  if (root == null) {
    return 0;
  }
  int leftMaxDepth = maxDepth(root.left);
  int rightMaxDepth = maxDepth(root.right);
	// 左右节点深度 + 加上当前层
  return 1 + Math.max(leftMaxDepth, rightMaxDepth);
}

时间复杂度

因为会走完所有节点，所以为O(N)

空间复杂度

递归遍历所占的额外空间就是占用的栈帧内存，取决于数的高度h，平均情况下是O(logN)，最坏情况下数呈现链状，为O(N)，所以空间复杂度是O(h)