【力扣76】最小覆盖子串

题目

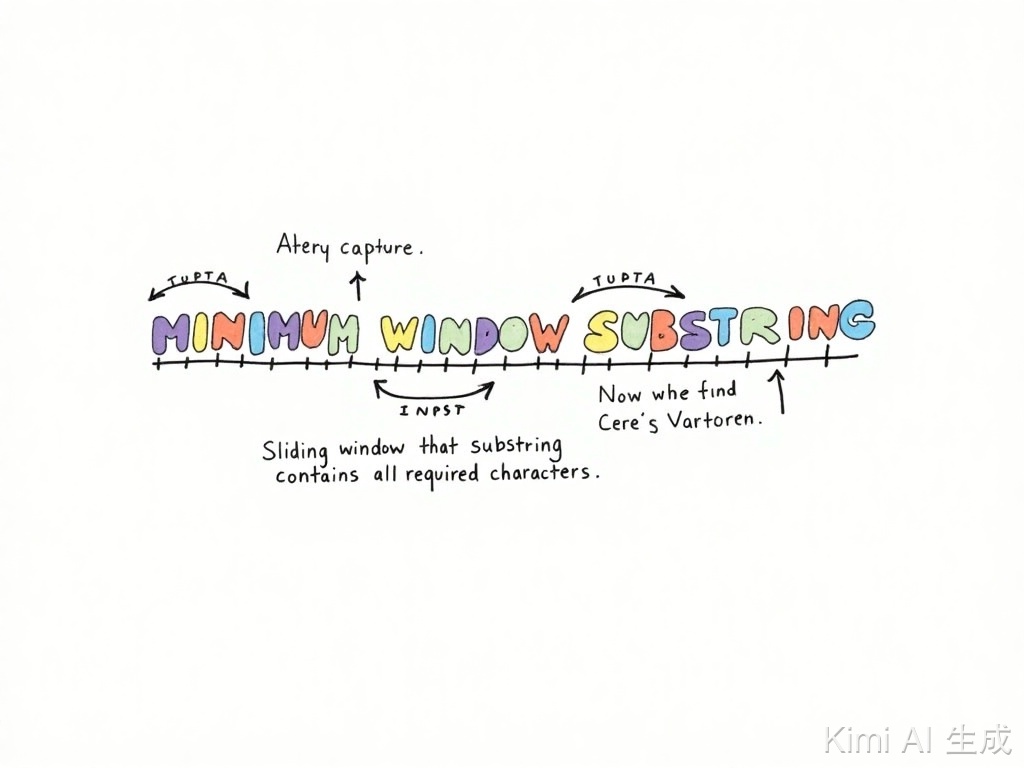
给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 "" 。

注意：

对于 t 中重复字符，我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
如果 s 中存在这样的子串，我们保证它是唯一的答案。

示例 1：

1
2
3

输入：s = "ADOBECODEBANC", t = "ABC"
输出："BANC"
解释：最小覆盖子串 "BANC" 包含来自字符串 t 的 'A'、'B' 和 'C'。

示例 2：

1
2
3

输入：s = "a", t = "a"
输出："a"
解释：整个字符串 s 是最小覆盖子串。

示例 3:

输入: s = "a", t = "aa"
输出: ""
解释: t 中两个字符 'a' 均应包含在 s 的子串中，
因此没有符合条件的子字符串，返回空字符串。

提示：

m == s.length
n == t.length
1 <= m, n <= 105
s 和 t 由英文字母组成

实现代码

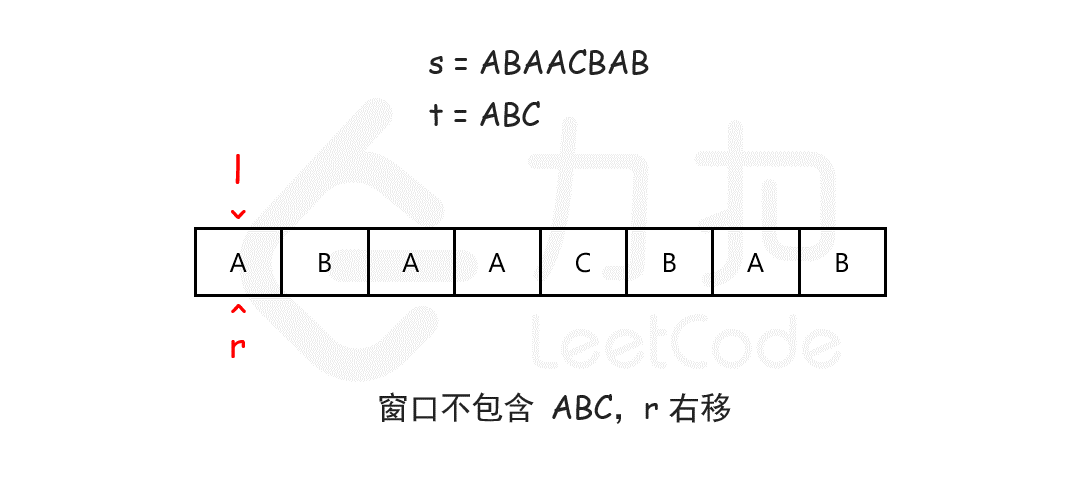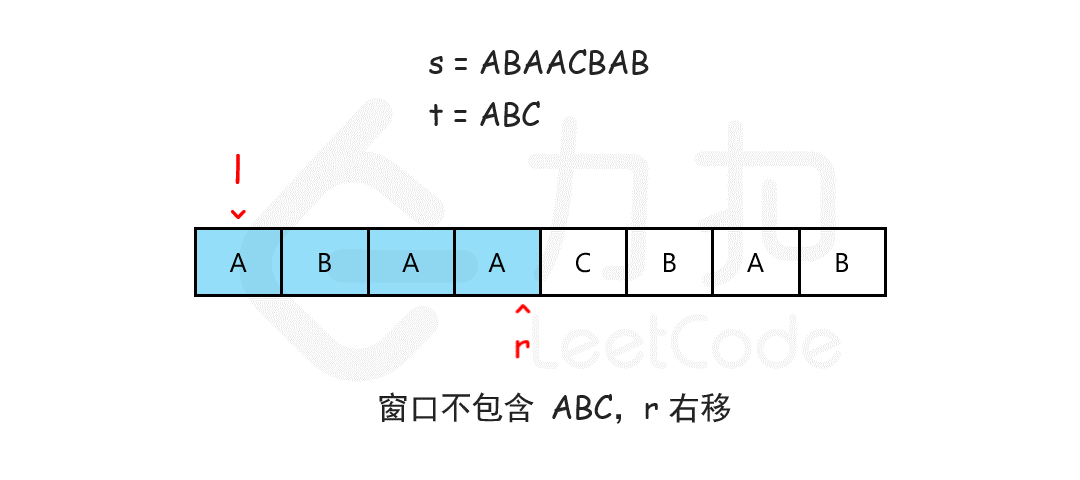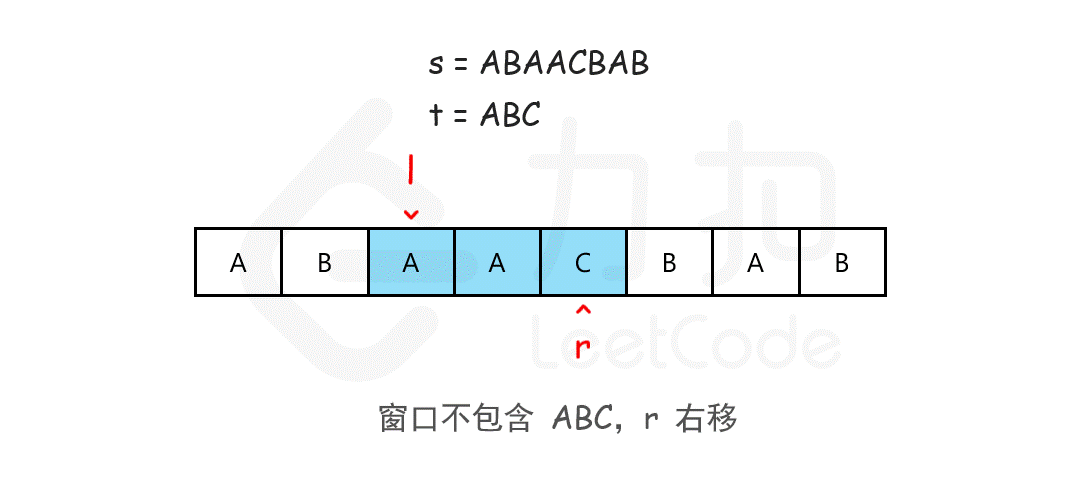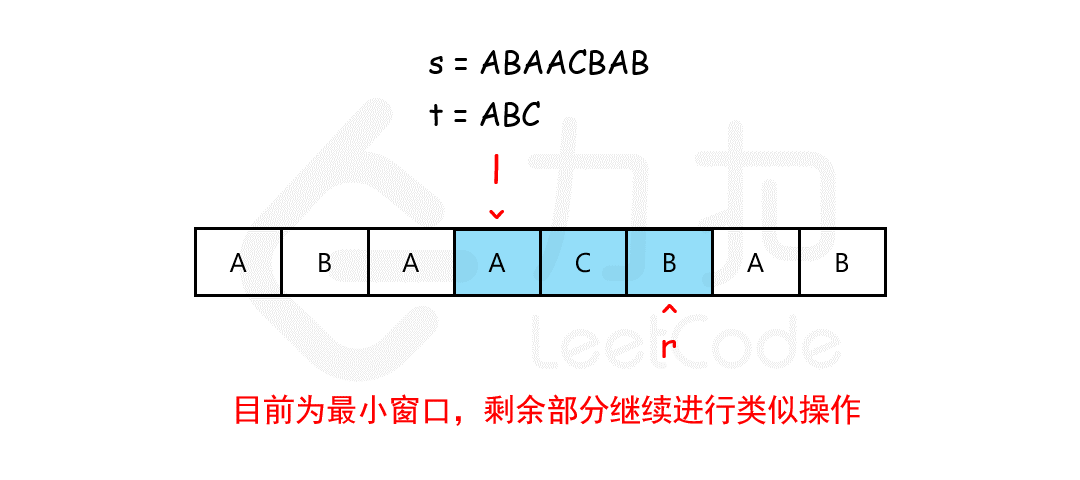
使用双指针方式，定义指针left、right，左闭右开，形成一个窗口，移动right扩张窗口，每次移动统计窗口内字符的出现次数，如果全部满足子串字符次数，则开始移动left收缩窗口，并记录最小覆盖串的大小，以此循环，直到right到末尾并且窗口不满足子串字符次数进行返回；

如下图（来自leetcode）；

76_fig1

class Solution {

  // 当前窗口内各字符的出现次数。
  Map<Character, Integer> windows = new HashMap<>();

  // 目标串  t  中各字符的出现次数
  Map<Character, Integer> subStrMap = new HashMap<>();

  public String minWindow(String s, String t) {

    int left = 0, right = 0;
    int n = 0, minLen = Integer.MAX_VALUE, start = 0;
    for (char c : t.toCharArray()) {
      subStrMap.put(c, subStrMap.getOrDefault(c, 0) + 1);
    }
    while (right < s.length()) {
      char rc = s.charAt(right);
      right++;
      // 统计匹配数
      n = nIncrease(rc, n);
      // 满足条件，开始收缩窗口
      while (n == subStrMap.size()) {
        // 刷新最小子串长度
        if (right - left < minLen) {
          start = left;
          minLen = right - left;
        }
        char lc = s.charAt(left);
        left++;
        // 窗口减少一个元素就跳出当前循环，进入外层循环补充元素
        n = nDecrease(lc, n);
      }

    }
    return minLen == Integer.MAX_VALUE ? "" : s.substring(start, start + minLen);
  }

  // 扩张窗口
  private int nIncrease(char c, int n) {

    if (subStrMap.containsKey(c)) {
      windows.put(c, windows.getOrDefault(c, 0) + 1);
      if (subStrMap.get(c).equals(windows.get(c))) {
        n++;
      }
    }
    return n;
  }

  // 收缩窗口
  private int nDecrease(char c, int n) {

    if (subStrMap.containsKey(c)) {
      if (subStrMap.get(c).equals(windows.get(c))) {
        n--;
      }
      windows.put(c, windows.get(c) - 1);
    }
    return n;
  }
}

代码讲解

while (right < s.length()) {
  char rc = s.charAt(right);
  // 位置A
  right++;
  // 统计匹配数
  n = nIncrease(rc, n);
  // 满足条件，开始收缩窗口
  while (n == subStrMap.size()) {
    // 刷新最小子串长度
    if (right - left < minLen) {
      start = left;
      minLen = right - left;
    }
    char lc = s.charAt(left);
    left++;
    // 窗口减少一个元素就跳出当前循环，进入外层循环补充元素
    n = nDecrease(lc, n);
  }
  // 位置B
  //right++;
}

为什么代码right++;要放在位置A，能不能放在位置B？

可以，但如果只是将right++从位置A移到位置B就会出问题，假设当前s = "a",t = "a",那么minLen = right - left;的计算结果就等于0，在最终输出的代码return minLen == Integer.MAX_VALUE ? "" : s.substring(start, start + minLen);中，因为s.substring是左闭右开的，[0,0)是0个元素，所以如果一定要放在位置A，还需要改以下代码：

// 刷新最小子串长度
if ((right + 1) - left < minLen) {
  start = left;
  minLen = (right + 1) - left;
}

因此，为了更方便的处理边界值，最好放在位置A

时间复杂度

最差的情况是left扫了一遍s，right扫了一遍s，那就是2*s，加上t的预处理，就是t+2*s，因为这里哈希表的插入、查询、增加操作的时间复杂度是O(1)，所以最终的时间复杂度是O(t+s)

空间复杂度

额外空间left、right和两个哈希表，left和right的空间复杂度是O(1)可以不计，因为哈希表是存放t字符的，大小取决于t中不同字符的个数m（m最大为整个字符集大小），那么空间复杂度就是O(m)；

扩展

放一下labuladong大佬关于滑动窗口算法的模板代码：

// 滑动窗口算法伪码框架
void slidingWindow(String s) {
  // 用合适的数据结构记录窗口中的数据，根据具体场景变通
  // 比如说，我想记录窗口中元素出现的次数，就用 map
  // 如果我想记录窗口中的元素和，就可以只用一个 int
  Object window = ...

    int left = 0, right = 0;
  while (right < s.length()) {
    // c 是将移入窗口的字符
    char c = s[right];
    window.add(c)
      // 增大窗口
      right++;
    // 进行窗口内数据的一系列更新
    ...

      // *** debug 输出的位置 ***
      // 注意在最终的解法代码中不要 print
      // 因为 IO 操作很耗时，可能导致超时
      printf("window: [%d, %d)\n", left, right);
    // ***********************

    // 判断左侧窗口是否要收缩
    while (left < right && window needs shrink) {
      // d 是将移出窗口的字符
      char d = s[left];
      window.remove(d)
        // 缩小窗口
        left++;
      // 进行窗口内数据的一系列更新
      ...
    }
  }
}