【力扣45】跳跃游戏II

题目

给定一个长度为 n 的 0 索引整数数组 nums。初始位置在下标 0。

每个元素 nums[i] 表示从索引 i 向后跳转的最大长度。换句话说，如果你在索引 i 处，你可以跳转到任意 (i + j) 处：

• 0 <= j <= nums[i] 且
• i + j < n

返回到达 n - 1 的最小跳跃次数。测试用例保证可以到达 n - 1。

示例 1:

输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
     从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。

示例 2:

输入: nums = [2,3,0,1,4]
输出: 2

提示:

• 1 <= nums.length <= 104
• 0 <= nums[i] <= 1000
• 题目保证可以到达 n - 1

实现代码

class Solution {

    public int jump(int[] nums) {
        
        int maxSpan = 0, end = 0, step = 0;
        if(nums.length == 1){
            return 0;
        }
        for (int i = 0; i < nums.length; i++) {
            maxSpan = Math.max(maxSpan, nums[i] + i);
            // 说明end就是当前最大跨度
            if(i == end){
                step ++;
                end = maxSpan;
                if(maxSpan >= nums.length-1){
                    return step;
                }
            }
        }
        return -1;
    }
}

核心思路

可以想象为飞行棋游戏，每次掷骰子肯定是想办法走的更远，比较好的是最大点数6，但更幸运的方式是落的位置是往前再进x步奖励，想一想，如果当前点数是2，并且往前进2点后的奖励是往前进5步，那是不是比6更好，贪心算法就是这个思路，一直往前进，在可达范围内尽量走的更远，如下：

假设数组nums = [2, 3, 1, 1, 4, 2]

i = 0

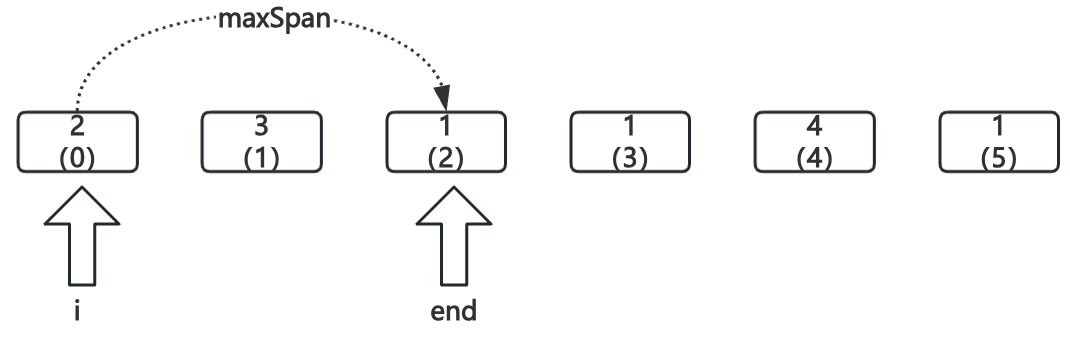
因为maxSpan = 0, end = 0，所以i == end，step加1，更新step = 1，更新end = 2, maxSpan = 2；

i = 1

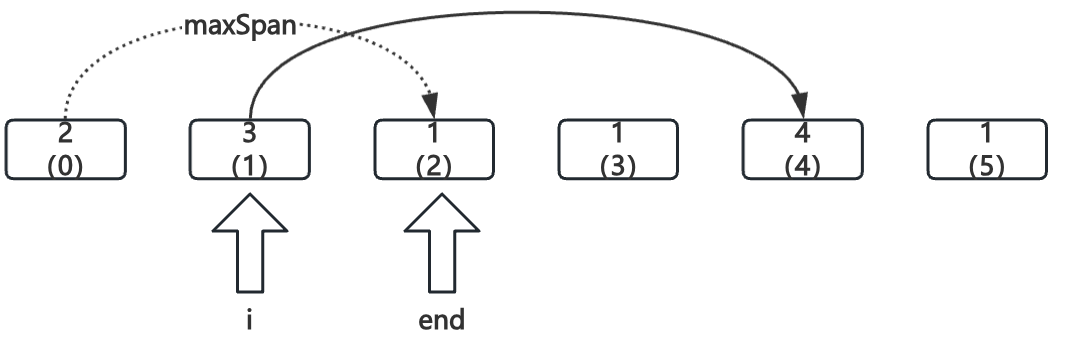
能跳到索引4位置，比当前的maxSpan大，更新maxSpan = 4

i = 2

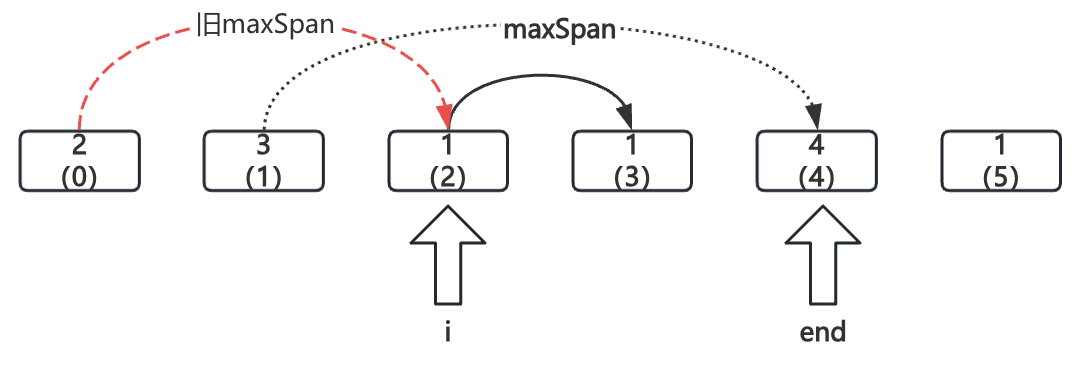
到达end点，step加1，step = 2，覆盖范围仍在数组内，更新end = 4

i = 3

没超过4，保存不变

i = 4

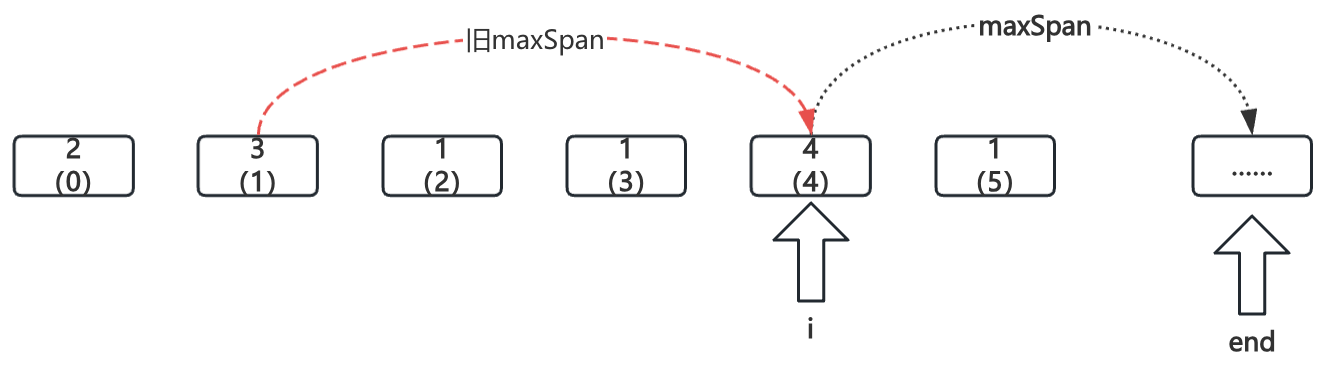
到达end点，step加1，更新step = 3，前进4格，超过数组索引，直接返回；

时间复杂度

因为直接遍历一遍就能找到，所以时间复杂度为O(n)

空间复杂度

主要的额外空间消耗来自变量maxSpan、end、step，所以空间复杂度为O(1)